Задача 1. Расчет стержней постоянного поперечного сечения при растяжении-сжатии.
Пример
Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) определить грузоподъемность стержня, если [σ]=240 МПа; 3) определить полное удлинение стержня, если Е=2×105 МПа![Задача 1. Расчет стержней постоянного поперечного сечения при растяжении-сжатии. Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) определить грузоподъемность стержня, если [σ]=240 МПа; 3) определить полное удлинение стержня, если Е=2∙105 МПа]( "Задача 1. Расчет стержней постоянного поперечного сечения при растяжении-сжатии. Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) определить грузоподъемность стержня, если [σ]=240 МПа; 3) определить полное удлинение стержня, если Е=2∙105 МПа")
250 р
Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) определить грузоподъемность стержня, если [σ]=240 МПа; 3) определить полное удлинение стержня, если Е=2×105 МПа
![Задача 1. Расчет стержней постоянного поперечного сечения при растяжении-сжатии. Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) определить грузоподъемность стержня, если [σ]=240 МПа; 3) определить полное удлинение стержня, если Е=2∙105 МПа](06/1.jpg "Задача 1. Расчет стержней постоянного поперечного сечения при растяжении-сжатии. Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) определить грузоподъемность стержня, если [σ]=240 МПа; 3) определить полное удлинение стержня, если Е=2∙105 МПа")
Задача 1.
Пример
Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) построить эпюры нормальных напряжений; 3) построить эпюры перемещений сечений стержня и определить полное удлинение стержня, если Е=2*105 МПа; 4) определить грузоподъемность стержня из условия [F]=A[σ], если [σ]=240 МПа. Данные взять из таблицы 1![Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) построить эпюры нормальных напряжений; 3) построить эпюры перемещений сечений стержня и определить полное удлинение стержня, если Е=2*10^5 МПа; 4) определить грузоподъемность стержня из условия [F]=A[σ], если [σ]=240 МПа. Данные взять из таблицы 1]( "Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) построить эпюры нормальных напряжений; 3) построить эпюры перемещений сечений стержня и определить полное удлинение стержня, если Е=2*10^5 МПа; 4) определить грузоподъемность стержня из условия [F]=A[σ], если [σ]=240 МПа. Данные взять из таблицы 1")
300 р
Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) построить эпюры нормальных напряжений; 3) построить эпюры перемещений сечений стержня и определить полное удлинение стержня, если Е=2*105 МПа; 4) определить грузоподъемность стержня из условия [F]=A[σ], если [σ]=240 МПа. Данные взять из таблицы 1
![Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) построить эпюры нормальных напряжений; 3) построить эпюры перемещений сечений стержня и определить полное удлинение стержня, если Е=2*10^5 МПа; 4) определить грузоподъемность стержня из условия [F]=A[σ], если [σ]=240 МПа. Данные взять из таблицы 1](06/1_1.jpg "Для стального стержня круглого поперечного сечения диаметром D требуется: 1) построить эпюры продольной силы; 2) построить эпюры нормальных напряжений; 3) построить эпюры перемещений сечений стержня и определить полное удлинение стержня, если Е=2*10^5 МПа; 4) определить грузоподъемность стержня из условия [F]=A[σ], если [σ]=240 МПа. Данные взять из таблицы 1")
Задача 1.
Схемы к задаче 1
![Задача 1. Схемы к задаче 1]( "Задача 1. Схемы к задаче 1")
Схемы к задаче 1
Задача 2. Расчет стержней постоянного поперечного сечения при растяжении-сжатии с распределенной нагрузкой.
Консольный стержень нагружен равномерно распределенными нагрузками интенсивностью q1 и q2 и сосредоточенными силами F1 и F2. Построить эпюру нормальной силы
![Задача 2. Расчет стержней постоянного поперечного сечения при растяжении-сжатии с распределенной нагрузкой. Консольный стержень нагружен равномерно распределенными нагрузками интенсивностью q1 и q2 и сосредоточенными силами F1 и F2. Построить эпюру нормальной силы]( "Задача 2. Расчет стержней постоянного поперечного сечения при растяжении-сжатии с распределенной нагрузкой. Консольный стержень нагружен равномерно распределенными нагрузками интенсивностью q1 и q2 и сосредоточенными силами F1 и F2. Построить эпюру нормальной силы")
250 р
Пример
Консольный стержень нагружен равномерно распределенными нагрузками интенсивностью q1 и q2 и сосредоточенными силами F1 и F2. Построить эпюру нормальной силы
Задача 2.
Схемы к задаче 2
![Задача 2. Схемы к задаче 2]( "Задача 2. Схемы к задаче 2")
Схемы к задаче 2
6. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ.
Пример
Для двух балок (двухопорной и консольной)
1. Построить эпюры поперечных сил «Q» и изгибающих моментов «Mи», если каждая нагружена сосредоточенной силой F, сосредоточенным моментом M и равномерно распределенной нагрузкой интенсивностью q. Длина пролета балок – L.
2. Определить из условия прочности по нормальным напряжениям размеры поперечного сечения балки в соответствии с заданием (круга диаметром D, прямоугольника с соотношением сторон h:b=2:1; квадрата со стороной а; профиля двутавровой балки; швеллера)![6. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ. Для двух балок (двухопорной и консольной). 1. Построить эпюры поперечных сил «Q» и изгибающих моментов «Mи», если каждая нагружена сосредоточенной силой F, сосредоточенным моментом M и равномерно распределенной нагрузкой интенсивностью q. Длина пролета балок – L. 2. Определить из условия прочности по нормальным напряжениям размеры поперечного сечения балки в соответствии с заданием (круга диаметром D, прямоугольника с соотношением сторон h:b=2:1; квадрата со стороной а; профиля двутавровой балки; швеллера)]( "6. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ. Для двух балок (двухопорной и консольной). 1. Построить эпюры поперечных сил «Q» и изгибающих моментов «Mи», если каждая нагружена сосредоточенной силой F, сосредоточенным моментом M и равномерно распределенной нагрузкой интенсивностью q. Длина пролета балок – L. 2. Определить из условия прочности по нормальным напряжениям размеры поперечного сечения балки в соответствии с заданием (круга диаметром D, прямоугольника с соотношением сторон h:b=2:1; квадрата со стороной а; профиля двутавровой балки; швеллера)")
350 р
Для двух балок (двухопорной и консольной)
1. Построить эпюры поперечных сил «Q» и изгибающих моментов «Mи», если каждая нагружена сосредоточенной силой F, сосредоточенным моментом M и равномерно распределенной нагрузкой интенсивностью q. Длина пролета балок – L.
2. Определить из условия прочности по нормальным напряжениям размеры поперечного сечения балки в соответствии с заданием (круга диаметром D, прямоугольника с соотношением сторон h:b=2:1; квадрата со стороной а; профиля двутавровой балки; швеллера)
Варианты к расчетным схемам балок. Таблица 1
• консольная
• двухопорная
• Квадрат
• Двутавр
• Прямоугольник![Варианты к расчетным схемам балок. Таблица 1; консольная; двухопорная; Квадрат; Двутавр; Прямоугольник]( "Варианты к расчетным схемам балок. Таблица 1; консольная; двухопорная; Квадрат; Двутавр; Прямоугольник")
350 р
Пример
• консольная
• двухопорная
• Квадрат
• Двутавр
• Прямоугольник
Задача 7. Определение внутренних усилий в симметричных балках при плоском поперечном изгибе.
На симметричную балку действуют симметричная (а) и кососимметричная (б) нагрузки. Требуется построить эпюры поперечной силы и изгибающего момента
![Задача 7. Определение внутренних усилий в симметричных балках при плоском поперечном изгибе. На симметричную балку действуют симметричная (а) и кососимметричная (б) нагрузки. Требуется построить эпюры поперечной силы и изгибающего момента]( "Задача 7. Определение внутренних усилий в симметричных балках при плоском поперечном изгибе. На симметричную балку действуют симметричная (а) и кососимметричная (б) нагрузки. Требуется построить эпюры поперечной силы и изгибающего момента")
350 р
Пример
На симметричную балку действуют симметричная (а) и кососимметричная (б) нагрузки. Требуется построить эпюры поперечной силы и изгибающего момента
Задача 2.
Пример
Ступенчатый брус нагружен силами P1, P2 и P3, направленными вдоль его оси. Заданы длины участков a, b, c и площади их поперечных сечений A1 и A2. Модуль упругости материала E=2*105 МПа, предел текучести σТ=240 МПа и запас прочности по отношению к пределу текучести nТ=1.5.
Требуется: 1) построить эпюры продольных сил N, напряжений σ и продольных перемещений Δ; 2) проверить, выполняется ли условие прочности![Задача 2. Ступенчатый брус нагружен силами P1, P2 и P3, направленными вдоль его оси. Заданы длины участков a, b, c и площади их поперечных сечений A1 и A2. Модуль упругости материала E=2*10^5 МПа, предел текучести σТ=240 МПа и запас прочности по отношению к пределу текучести nТ=1.5. Требуется: 1) построить эпюры продольных сил N, напряжений σ и продольных перемещений Δ; 2) проверить, выполняется ли условие прочности. Расчетные схемы выбираются на рис. 2, числовые данные берутся из таблицы 2]( "Задача 2. Ступенчатый брус нагружен силами P1, P2 и P3, направленными вдоль его оси. Заданы длины участков a, b, c и площади их поперечных сечений A1 и A2. Модуль упругости материала E=2*10^5 МПа, предел текучести σТ=240 МПа и запас прочности по отношению к пределу текучести nТ=1.5. Требуется: 1) построить эпюры продольных сил N, напряжений σ и продольных перемещений Δ; 2) проверить, выполняется ли условие прочности. Расчетные схемы выбираются на рис. 2, числовые данные берутся из таблицы 2")
300 р
Ступенчатый брус нагружен силами P1, P2 и P3, направленными вдоль его оси. Заданы длины участков a, b, c и площади их поперечных сечений A1 и A2. Модуль упругости материала E=2*105 МПа, предел текучести σТ=240 МПа и запас прочности по отношению к пределу текучести nТ=1.5.
Требуется: 1) построить эпюры продольных сил N, напряжений σ и продольных перемещений Δ; 2) проверить, выполняется ли условие прочности
Задача 3.
Пример
Для заданной двухопорной балки (рис. 3) при указанных на схеме нагрузках и размерах требуется:
1. Определить опорные реакции.
2. Построить эпюры поперечных сил и изгибающих моментов.
3. Из условия прочности подобрать двутавровое сечение балки, приняв [σ]=160 МПа.
Данные взять из таблицы 3. Таблица 3![Задача 3. Для заданной двухопорной балки (рис. 3) при указанных на схеме нагрузках и размерах требуется: 1. Определить опорные реакции. 2. Построить эпюры поперечных сил и изгибающих моментов. 3. Из условия прочности подобрать двутавровое сечение балки, приняв [σ]=160 МПа. Данные взять из таблицы 3. Таблица 3]( "Задача 3. Для заданной двухопорной балки (рис. 3) при указанных на схеме нагрузках и размерах требуется: 1. Определить опорные реакции. 2. Построить эпюры поперечных сил и изгибающих моментов. 3. Из условия прочности подобрать двутавровое сечение балки, приняв [σ]=160 МПа. Данные взять из таблицы 3. Таблица 3")
350 р
Для заданной двухопорной балки (рис. 3) при указанных на схеме нагрузках и размерах требуется:
1. Определить опорные реакции.
2. Построить эпюры поперечных сил и изгибающих моментов.
3. Из условия прочности подобрать двутавровое сечение балки, приняв [σ]=160 МПа.
Данные взять из таблицы 3. Таблица 3
![Задача 3. Для заданной двухопорной балки (рис. 3) при указанных на схеме нагрузках и размерах требуется: 1. Определить опорные реакции. 2. Построить эпюры поперечных сил и изгибающих моментов. 3. Из условия прочности подобрать двутавровое сечение балки, приняв [σ]=160 МПа. Данные взять из таблицы 3. Таблица 3](06/3_1.jpg "Задача 3. Для заданной двухопорной балки (рис. 3) при указанных на схеме нагрузках и размерах требуется: 1. Определить опорные реакции. 2. Построить эпюры поперечных сил и изгибающих моментов. 3. Из условия прочности подобрать двутавровое сечение балки, приняв [σ]=160 МПа. Данные взять из таблицы 3. Таблица 3")
ЗАДАЧА № 4.
Пример
Для двух заданных сечений, состоящих из нескольких элементов или имеющих вырезы, определить положение главных центральных осей инерции и вычислить величины моментов инерции относительно этих осей. При расчете сечения, состоящего из прокатных профилей, уголок следует принимать в соответствии с заданными размерами; он может быть равнобоким или неравнобоким![ЗАДАЧА № 4
Для двух заданных сечений, состоящих из нескольких элементов или имеющих вырезы, определить положение главных центральных осей инерции и вычислить величины моментов инерции относительно этих осей. Первое сечение для расчета выбирается по рис.8, второе - по рис.9. Размеры элементов сечений и номера прокатных профилей берутся из табл.4. При расчете сечения, состоящего из прокатных профилей, уголок следует принимать в соответствии с заданными размерами; он может быть равнобоким или неравнобоким]( "ЗАДАЧА № 4
Для двух заданных сечений, состоящих из нескольких элементов или имеющих вырезы, определить положение главных центральных осей инерции и вычислить величины моментов инерции относительно этих осей. Первое сечение для расчета выбирается по рис.8, второе - по рис.9. Размеры элементов сечений и номера прокатных профилей берутся из табл.4. При расчете сечения, состоящего из прокатных профилей, уголок следует принимать в соответствии с заданными размерами; он может быть равнобоким или неравнобоким")
600 р
Для двух заданных сечений, состоящих из нескольких элементов или имеющих вырезы, определить положение главных центральных осей инерции и вычислить величины моментов инерции относительно этих осей. При расчете сечения, состоящего из прокатных профилей, уголок следует принимать в соответствии с заданными размерами; он может быть равнобоким или неравнобоким
Задача 4.
Пример
Для заданной консольной балки (рис. 4) при указанных на схеме нагрузках и размерах требуется:
1. Построить эпюры поперечных сил и изгибающих моментов.
2. Подобрать прямоугольное сечение при соотношении сторон h=2b, приняв [σ]=8,3 МПа (сосна).
Данные для решения задачи взять из таблицы 3![Задача 4. Для заданной консольной балки (рис. 4) при указанных на схеме нагрузках и размерах требуется: 1. Построить эпюры поперечных сил и изгибающих моментов. 2. Подобрать прямоугольное сечение при соотношении сторон h=2b, приняв [σ]=8,3 МПа (сосна). Данные для решения задачи взять из таблицы 3]( "Задача 4. Для заданной консольной балки (рис. 4) при указанных на схеме нагрузках и размерах требуется: 1. Построить эпюры поперечных сил и изгибающих моментов. 2. Подобрать прямоугольное сечение при соотношении сторон h=2b, приняв [σ]=8,3 МПа (сосна). Данные для решения задачи взять из таблицы 3")
350 р
Для заданной консольной балки (рис. 4) при указанных на схеме нагрузках и размерах требуется:
1. Построить эпюры поперечных сил и изгибающих моментов.
2. Подобрать прямоугольное сечение при соотношении сторон h=2b, приняв [σ]=8,3 МПа (сосна).
Данные для решения задачи взять из таблицы 3
![Задача 4. Для заданной консольной балки (рис. 4) при указанных на схеме нагрузках и размерах требуется: 1. Построить эпюры поперечных сил и изгибающих моментов. 2. Подобрать прямоугольное сечение при соотношении сторон h=2b, приняв [σ]=8,3 МПа (сосна). Данные для решения задачи взять из таблицы 3](06/3_2.jpg "Задача 4. Для заданной консольной балки (рис. 4) при указанных на схеме нагрузках и размерах требуется: 1. Построить эпюры поперечных сил и изгибающих моментов. 2. Подобрать прямоугольное сечение при соотношении сторон h=2b, приняв [σ]=8,3 МПа (сосна). Данные для решения задачи взять из таблицы 3")
ЗАДАЧА № 5.
Пример
Для заданных схем балок требуется: Построить эпюры поперечных сил и изгибающих моментов; подобрать поперечные сечения балок по следующим вариантам: а) для стальной балки - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b=2; круглое - диаметром d; б) для чугунной балки - форму сечения выбрать по рис.14, определить размеры сечения из условия прочности по допускаемым напряжениям; в) для стальной балки - сечение, состоящее из двух швеллеров. Для стальной двутавровой балки (вариант а) и чугунной балки (вариант б) построить эпюры распределения нормальных напряжений по высоте сечения![ЗАДАЧА № 5.
Для заданных схем балок требуется: Построить эпюры поперечных сил и изгибающих моментов; подобрать поперечные сечения балок по следующим вариантам: а) для стальной балки - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b=2; круглое - диаметром d; б) для чугунной балки - форму сечения выбрать по рис.14, определить размеры сечения из условия прочности по допускаемым напряжениям; в) для стальной балки - сечение, состоящее из двух швеллеров. Для стальной двутавровой балки (вариант а) и чугунной балки (вариант б) построить эпюры распределения нормальных напряжений по высоте сечения]( "ЗАДАЧА № 5.
Для заданных схем балок требуется: Построить эпюры поперечных сил и изгибающих моментов; подобрать поперечные сечения балок по следующим вариантам: а) для стальной балки - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b=2; круглое - диаметром d; б) для чугунной балки - форму сечения выбрать по рис.14, определить размеры сечения из условия прочности по допускаемым напряжениям; в) для стальной балки - сечение, состоящее из двух швеллеров. Для стальной двутавровой балки (вариант а) и чугунной балки (вариант б) построить эпюры распределения нормальных напряжений по высоте сечения")
Для заданных схем балок требуется: Построить эпюры поперечных сил и изгибающих моментов; подобрать поперечные сечения балок по следующим вариантам: а) для стальной балки - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b=2; круглое - диаметром d; б) для чугунной балки - форму сечения выбрать по рис.14, определить размеры сечения из условия прочности по допускаемым напряжениям; в) для стальной балки - сечение, состоящее из двух швеллеров. Для стальной двутавровой балки (вариант а) и чугунной балки (вариант б) построить эпюры распределения нормальных напряжений по высоте сечения
Числовые данные берутся из табл. 5, расчетные схемы - по рис.13.
Рис. 13. Расчетные схемы балок к задаче № 5
Рис. 14. Формы сечений чугунных балок к задаче № 5
Задача 4.
Пример
К стальному валу приложены четыре момента (рис.4.1). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180 и 200мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания (на 1 пог. м)![Задача 4.
К стальному валу приложены четыре момента (рис.4.1). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180 и 200мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания (на 1 пог. м)]( "Задача 4.
К стальному валу приложены четыре момента (рис.4.1). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180 и 200мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания (на 1 пог. м)")
350 р
К стальному валу приложены четыре момента (рис.4.1). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180 и 200мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания (на 1 пог. м)
![Задача 4.
К стальному валу приложены четыре момента (рис.4.1). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180 и 200мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания (на 1 пог. м)](06/drugoe_kruchenie.jpg "Задача 4.
К стальному валу приложены четыре момента (рис.4.1). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей величины, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180 и 200мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания (на 1 пог. м)")
Задача 5.
Пример
К стальному валу приложены скручивающие моменты: М1, М2, М3, М4, (рис. 5). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания.![Задача 5. К стальному валу приложены скручивающие моменты: М1, М2, М3, М4, (рис. 5). Требуется: 1) построить эпюру крутящих моментов; 2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм; 3) построить эпюру углов закручивания; 4) найти наибольший относительный угол закручивания. Данные взять из таблицы 4]( "Задача 5. К стальному валу приложены скручивающие моменты: М1, М2, М3, М4, (рис. 5). Требуется: 1) построить эпюру крутящих моментов; 2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм; 3) построить эпюру углов закручивания; 4) найти наибольший относительный угол закручивания. Данные взять из таблицы 4")
350 р
К стальному валу приложены скручивающие моменты: М1, М2, М3, М4, (рис. 5). Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания.
![Задача 5. К стальному валу приложены скручивающие моменты: М1, М2, М3, М4, (рис. 5). Требуется: 1) построить эпюру крутящих моментов; 2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм; 3) построить эпюру углов закручивания; 4) найти наибольший относительный угол закручивания. Данные взять из таблицы 4](06/4_1.jpg "Задача 5. К стальному валу приложены скручивающие моменты: М1, М2, М3, М4, (рис. 5). Требуется: 1) построить эпюру крутящих моментов; 2) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40,45, 50, 60, 70, 80, 90, 100 мм; 3) построить эпюру углов закручивания; 4) найти наибольший относительный угол закручивания. Данные взять из таблицы 4")
Задача 1.
Пример
Построение эпюр внутренних силовых факторов при растяжении (сжатии).
Для стержня, нагруженного сосредоточенными силами и равномерно распределенной нагрузкой, построить эпюру продольной силы ЭN (в долях Р)![Задача 1. Построение эпюр внутренних силовых факторов при растяжении (сжатии). Для стержня, нагруженного сосредоточенными силами и равномерно распределенной нагрузкой, построить эпюру продольной силы ЭN (в долях Р)]( "Задача 1. Построение эпюр внутренних силовых факторов при растяжении (сжатии). Для стержня, нагруженного сосредоточенными силами и равномерно распределенной нагрузкой, построить эпюру продольной силы ЭN (в долях Р)")
200 р
Построение эпюр внутренних силовых факторов при растяжении (сжатии).
Для стержня, нагруженного сосредоточенными силами и равномерно распределенной нагрузкой, построить эпюру продольной силы ЭN (в долях Р)
Задача 5.
Пример
Консольная балка постоянного круглого поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь 50Х, термообработка нормализация, допускаемое напряжение изгиба [σ]=160 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый диаметр балки из условия прочности на изгиб по нормальным напряжениям с округлением по стандарту (Приложение 1)![Задача 5.
Консольная балка постоянного круглого поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М.
Материал балки сталь 50Х, термообработка нормализация, допускаемое напряжение изгиба [σ]=160 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый диаметр балки из условия прочности на изгиб по нормальным напряжениям с округлением по стандарту (Приложение 1)]( "Задача 5.
Консольная балка постоянного круглого поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М.
Материал балки сталь 50Х, термообработка нормализация, допускаемое напряжение изгиба [σ]=160 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый диаметр балки из условия прочности на изгиб по нормальным напряжениям с округлением по стандарту (Приложение 1)")
350 р
Консольная балка постоянного круглого поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь 50Х, термообработка нормализация, допускаемое напряжение изгиба [σ]=160 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый диаметр балки из условия прочности на изгиб по нормальным напряжениям с округлением по стандарту (Приложение 1)
![Задача 5.
Консольная балка постоянного круглого поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М.
Материал балки сталь 50Х, термообработка нормализация, допускаемое напряжение изгиба [σ]=160 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый диаметр балки из условия прочности на изгиб по нормальным напряжениям с округлением по стандарту (Приложение 1)](06/zadacha_5.jpg "Задача 5.
Консольная балка постоянного круглого поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М.
Материал балки сталь 50Х, термообработка нормализация, допускаемое напряжение изгиба [σ]=160 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый диаметр балки из условия прочности на изгиб по нормальным напряжениям с округлением по стандарту (Приложение 1)")
Задача 6.
Пример
Двухопорная балка постоянного поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь Ст 4, допускаемое напряжение изгиба [σ]=120 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый осевой момент сопротивления поперечного сечения балки из условия прочности на изгиб по нормальным напряжениям и размеры поперечного сечения при различных его формах:![Задача 6.
Двухопорная балка постоянного поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь Ст 4, допускаемое напряжение изгиба [σ]=120 Н/мм 2 (МПа).
Требуется: 1) Построить эпюры поперечных сил и изгибающих моментов. 2) Определить необходимый осевой момент сопротивления поперечного сечения балки из условия прочности на изгиб по нормальным напряжениям и размеры поперечного сечения при различных его формах:]( "Задача 6.
Двухопорная балка постоянного поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь Ст 4, допускаемое напряжение изгиба [σ]=120 Н/мм 2 (МПа).
Требуется: 1) Построить эпюры поперечных сил и изгибающих моментов. 2) Определить необходимый осевой момент сопротивления поперечного сечения балки из условия прочности на изгиб по нормальным напряжениям и размеры поперечного сечения при различных его формах:")
450 р
Двухопорная балка постоянного поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь Ст 4, допускаемое напряжение изгиба [σ]=120 Н/мм2 (МПа).
Требуется:
1) Построить эпюры поперечных сил и изгибающих моментов.
2) Определить необходимый осевой момент сопротивления поперечного сечения балки из условия прочности на изгиб по нормальным напряжениям и размеры поперечного сечения при различных его формах:
![Задача 6.
Двухопорная балка постоянного поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь Ст 4, допускаемое напряжение изгиба [σ]=120 Н/мм 2 (МПа).
Требуется: 1) Построить эпюры поперечных сил и изгибающих моментов. 2) Определить необходимый осевой момент сопротивления поперечного сечения балки из условия прочности на изгиб по нормальным напряжениям и размеры поперечного сечения при различных его формах:](06/zadacha_6.jpg "Задача 6.
Двухопорная балка постоянного поперечного сечения нагружена равномерно распределенной нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом М. Материал балки сталь Ст 4, допускаемое напряжение изгиба [σ]=120 Н/мм 2 (МПа).
Требуется: 1) Построить эпюры поперечных сил и изгибающих моментов. 2) Определить необходимый осевой момент сопротивления поперечного сечения балки из условия прочности на изгиб по нормальным напряжениям и размеры поперечного сечения при различных его формах:")
Задача 6.
Пример
а) Круглое поперечное сечение. Диаметр округлить до стандартной величины
б) Кольцевое поперечное сечение при отношении внутреннего диаметра к наружному α=d/D=0,8. Наружный диаметр D округлить до стандартной величины
в) Квадратное поперечное сечение. Размер а стороны квадрата округлить до стандартной величины
г) Швеллер. Номер сечения подобрать по стандарту
д) Двутавр. Номер сечения подобрать по стандарту.
3) Сравнить массы балок при различных формах поперечных сечений![Задача 6.
а) Круглое поперечное сечение. Диаметр округлить до стандартной величины. б) Кольцевое поперечное сечение при отношении внутреннего диаметра к наружному α=d/D=0,8. Наружный диаметр D округлить до стандартной величины. в) Квадратное поперечное сечение. Размер а стороны квадрата округлить до стандартной величины.г) Швеллер. Номер сечения подобрать по стандарту. д) Двутавр. Номер сечения подобрать по стандарту. 3) Сравнить массы балок при различных формах поперечных сечений]( "Задача 6.
а) Круглое поперечное сечение. Диаметр округлить до стандартной величины. б) Кольцевое поперечное сечение при отношении внутреннего диаметра к наружному α=d/D=0,8. Наружный диаметр D округлить до стандартной величины. в) Квадратное поперечное сечение. Размер а стороны квадрата округлить до стандартной величины.г) Швеллер. Номер сечения подобрать по стандарту. д) Двутавр. Номер сечения подобрать по стандарту. 3) Сравнить массы балок при различных формах поперечных сечений")
450 р
а) Круглое поперечное сечение. Диаметр округлить до стандартной величины
б) Кольцевое поперечное сечение при отношении внутреннего диаметра к наружному α=d/D=0,8. Наружный диаметр D округлить до стандартной величины
в) Квадратное поперечное сечение. Размер а стороны квадрата округлить до стандартной величины
г) Швеллер. Номер сечения подобрать по стандарту
д) Двутавр. Номер сечения подобрать по стандарту.
3) Сравнить массы балок при различных формах поперечных сечений
Задача 6.
Пример
Подобрать прочные размеры и оценить экономичность подобранных сечений.
Двухопорная балка.
1. Вычертить схему балки с указанием числовых данных.
2. Определить внутренние усилия по участкам и построить эпюры Q и М с указанием характерных координат.
3. Из условия прочности подобрать прочные размеры поперечных сечений стальной балки: круглое (d), прямоугольное (h:b=2), квадратное (bxb) и двутавровое.
4. Оценить экономичность подобранных сечений![Задача 6.
Подобрать прочные размеры и оценить экономичность подобранных сечений.
Двухопорная балка.
1. Вычертить схему балки с указанием числовых данных.
2. Определить внутренние усилия по участкам и построить эпюры Q и М с указанием характерных координат.
3. Из условия прочности подобрать прочные размеры поперечных сечений стальной балки: круглое (d), прямоугольное (h:b=2), квадратное (bxb) и двутавровое.
4. Оценить экономичность подобранных сечений]( "Задача 6.
Подобрать прочные размеры и оценить экономичность подобранных сечений.
Двухопорная балка.
1. Вычертить схему балки с указанием числовых данных.
2. Определить внутренние усилия по участкам и построить эпюры Q и М с указанием характерных координат.
3. Из условия прочности подобрать прочные размеры поперечных сечений стальной балки: круглое (d), прямоугольное (h:b=2), квадратное (bxb) и двутавровое.
4. Оценить экономичность подобранных сечений")
450 р
Подобрать прочные размеры и оценить экономичность подобранных сечений.
Двухопорная балка.
1. Вычертить схему балки с указанием числовых данных.
2. Определить внутренние усилия по участкам и построить эпюры Q и М с указанием характерных координат.
3. Из условия прочности подобрать прочные размеры поперечных сечений стальной балки: круглое (d), прямоугольное (h:b=2), квадратное (bxb) и двутавровое.
4. Оценить экономичность подобранных сечений
Задача
Пример
Вдоль стального стержня круглого сечения действуют силы P1=100 кН и P2=2P1. Площадь сечений характерных участков А2=А, A1=2А.
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ. Рассчитать минимальную площадь сечения А, если коэффициент запаса прочности n=2, модуль упругости Е=200*109 Па, предельно допустимое напряжение при растяжении/сжатии [σ]=150 МПа, длина участка L=1 м![Вдоль стального стержня круглого сечения действуют силы P1=100 кН и P2=2P1. Площадь сечений характерных участков А2=А, A1=2А.
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ. Рассчитать минимальную площадь сечения А, если коэффициент запаса прочности n=2, модуль упругости Е=200*10^9 Па, предельно допустимое напряжение при растяжении/сжатии [σ]=150 МПа, длина участка L=1 м]( "Вдоль стального стержня круглого сечения действуют силы P1=100 кН и P2=2P1. Площадь сечений характерных участков А2=А, A1=2А.
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ. Рассчитать минимальную площадь сечения А, если коэффициент запаса прочности n=2, модуль упругости Е=200*10^9 Па, предельно допустимое напряжение при растяжении/сжатии [σ]=150 МПа, длина участка L=1 м")
350 р
Вдоль стального стержня круглого сечения действуют силы P1=100 кН и P2=2P1. Площадь сечений характерных участков А2=А, A1=2А.
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ. Рассчитать минимальную площадь сечения А, если коэффициент запаса прочности n=2, модуль упругости Е=200*109 Па, предельно допустимое напряжение при растяжении/сжатии [σ]=150 МПа, длина участка L=1 м
![Вдоль стального стержня круглого сечения действуют силы P1=100 кН и P2=2P1. Площадь сечений характерных участков А2=А, A1=2А.
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ. Рассчитать минимальную площадь сечения А, если коэффициент запаса прочности n=2, модуль упругости Е=200*10^9 Па, предельно допустимое напряжение при растяжении/сжатии [σ]=150 МПа, длина участка L=1 м](06/bilet.jpg "Вдоль стального стержня круглого сечения действуют силы P1=100 кН и P2=2P1. Площадь сечений характерных участков А2=А, A1=2А.
Построить эпюры продольных сил N, нормальных напряжений σ и перемещений δ. Рассчитать минимальную площадь сечения А, если коэффициент запаса прочности n=2, модуль упругости Е=200*10^9 Па, предельно допустимое напряжение при растяжении/сжатии [σ]=150 МПа, длина участка L=1 м")
Расчетно-графическая работа №1. Центральное растяжение
Пример
Для стержня переменного поперечного сечения (рис.2), соответствующего варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.2, находящегося под действием продольных нагрузок требуется:
1) построить эпюры продольных усилий;
2) построить эпюры напряжений;
3) построить эпюру перемещений;
4) определить наибольшую относительную деформацию в стержне![Расчетно-графическая работа №1. Центральное растяжение
Для стержня переменного поперечного сечения (рис.2), соответствующего варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.2, находящегося под действием продольных нагрузок требуется:
1) построить эпюры продольных усилий;
2) построить эпюры напряжений;
3) построить эпюру перемещений;
4) определить наибольшую относительную деформацию в стержне]( "Расчетно-графическая работа №1. Центральное растяжение
Для стержня переменного поперечного сечения (рис.2), соответствующего варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.2, находящегося под действием продольных нагрузок требуется:
1) построить эпюры продольных усилий;
2) построить эпюры напряжений;
3) построить эпюру перемещений;
4) определить наибольшую относительную деформацию в стержне")
350 р
Для стержня переменного поперечного сечения (рис.2), соответствующего варианту задания, с размерами и нагрузкой, выбранными по шифру из табл.2, находящегося под действием продольных нагрузок требуется:
1) построить эпюры продольных усилий;
2) построить эпюры напряжений;
3) построить эпюру перемещений;
4) определить наибольшую относительную деформацию в стержне
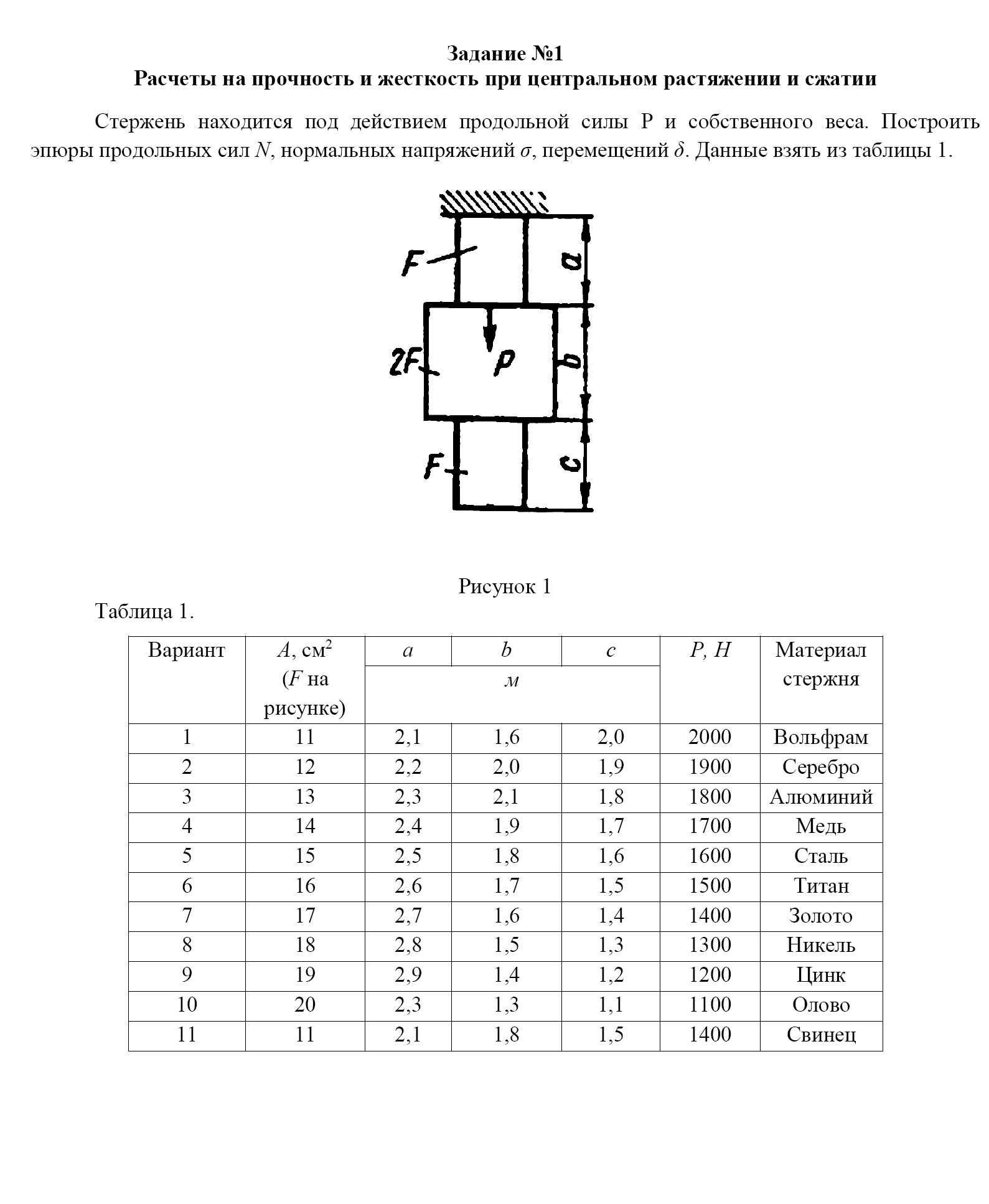
Задание №1
Расчеты на прочность и жесткость при центральном растяжении и сжатии Пример
Стержень находится под действием продольной силы P и собственного веса.
Построить эпюры продольных сил N, нормальных напряжений σ, перемещений δ.
Данные взять из таблицы 1
Материал стержня: Вольфрам Серебро Алюминий Медь Сталь Титан Золото Никель Цинк Олово Свинец![Задание №1
<br>Расчеты на прочность и жесткость при центральном растяжении и сжатии
<br>Стержень находится под действием продольной силы P и собственного веса.
<br>Построить эпюры продольных сил N, нормальных напряжений σ, перемещений δ.
<br>Данные взять из таблицы 1
<br>Материал стержня: Вольфрам Серебро Алюминий Медь Сталь Титан Золото Никель Цинк Олово Свинец]( "Задание №1
<br>Расчеты на прочность и жесткость при центральном растяжении и сжатии
<br>Стержень находится под действием продольной силы P и собственного веса.
<br>Построить эпюры продольных сил N, нормальных напряжений σ, перемещений δ.
<br>Данные взять из таблицы 1
<br>Материал стержня: Вольфрам Серебро Алюминий Медь Сталь Титан Золото Никель Цинк Олово Свинец")
Расчеты на прочность и жесткость при центральном растяжении и сжатии Пример
400 р
Стержень находится под действием продольной силы P и собственного веса.
Построить эпюры продольных сил N, нормальных напряжений σ, перемещений δ.
Данные взять из таблицы 1
Материал стержня: Вольфрам Серебро Алюминий Медь Сталь Титан Золото Никель Цинк Олово Свинец
Задание №2
Расчеты на прочность и жесткость при кручении брусьев круглого поперечного сечения Пример
Для ступенчатого стержня круглого сечения необходимо построить эпюры крутящих моментов Mкр, касательных напряжений τmax, углов закручивания φ.
Данные взять из таблицы 2.
D1 D2 D3 2d 4d 5d 6d 8d
L1 L2 L3 2l 3l 4l 6l 8l 10l
M1 M2 M3 2ml 3ml 4ml 5ml 6ml![Задание №2
<br>Расчеты на прочность и жесткость при кручении брусьев круглого поперечного сечения
<br>Для ступенчатого стержня круглого сечения необходимо построить эпюры крутящих
моментов Mкр, касательных напряжений τ<sub>max</sub>, углов закручивания φ.
<br>Данные взять из таблицы 2.
<br>D<sub>1</sub> D<sub>2</sub> D<sub>3</sub> 2d 4d 5d 6d 8d
<br>L<sub>1</sub> L<sub>2</sub> L<sub>3</sub> 2l 3l 4l 6l 8l 10l
<br>M<sub>1</sub> M<sub>2</sub> M<sub>3</sub> 2ml 3ml 4ml 5ml 6ml]( "Задание №2
<br>Расчеты на прочность и жесткость при кручении брусьев круглого поперечного сечения
<br>Для ступенчатого стержня круглого сечения необходимо построить эпюры крутящих
моментов Mкр, касательных напряжений τ<sub>max</sub>, углов закручивания φ.
<br>Данные взять из таблицы 2.
<br>D<sub>1</sub> D<sub>2</sub> D<sub>3</sub> 2d 4d 5d 6d 8d
<br>L<sub>1</sub> L<sub>2</sub> L<sub>3</sub> 2l 3l 4l 6l 8l 10l
<br>M<sub>1</sub> M<sub>2</sub> M<sub>3</sub> 2ml 3ml 4ml 5ml 6ml")
Расчеты на прочность и жесткость при кручении брусьев круглого поперечного сечения Пример
400 р
Для ступенчатого стержня круглого сечения необходимо построить эпюры крутящих моментов Mкр, касательных напряжений τmax, углов закручивания φ.
Данные взять из таблицы 2.
D1 D2 D3 2d 4d 5d 6d 8d
L1 L2 L3 2l 3l 4l 6l 8l 10l
M1 M2 M3 2ml 3ml 4ml 5ml 6ml
Задание №3
Расчеты на прочность при прямом поперечном изгибе Пример
Для заданной схемы балки требуется построить эпюры поперечных сил Q и изгибающих моментов Mизг
Данные взять из таблицы 3.
Схема по рис.3
P, кН m, кН*м q, кН/м
![Задание №3
<br>Расчеты на прочность при прямом поперечном изгибе
<br>Для заданной схемы балки требуется построить эпюры поперечных сил Q и изгибающих
моментов M<sub>изг</sub>
<br>Данные взять из таблицы 3.
<br>Схема по рис.3
<br>P, кН m, кН*м q, кН/м]( "Задание №3
<br>Расчеты на прочность при прямом поперечном изгибе
<br>Для заданной схемы балки требуется построить эпюры поперечных сил Q и изгибающих
моментов M<sub>изг</sub>
<br>Данные взять из таблицы 3.
<br>Схема по рис.3
<br>P, кН m, кН*м q, кН/м")
Расчеты на прочность при прямом поперечном изгибе Пример
400 р
Для заданной схемы балки требуется построить эпюры поперечных сил Q и изгибающих моментов Mизг
Данные взять из таблицы 3.
Схема по рис.3
P, кН m, кН*м q, кН/м
chertegi@mail.ru